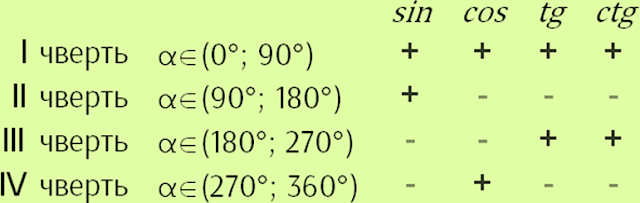Тригонометрія

Розв'яжіть вправи і здайте мені на перевірку.

Градуси і радіани

Напрям

Знаки функцій у чвертях

Основні формули

Перед коренем квадратним пишуть мінус тоді, коли функція у вказаній (у завданні) чверті від'ємна (див. вище знаки функцій у чвертях).

Клікніть на формули зведення. Картинка відкриється в новому вікні - так краще видно.

Формули зведення

Формулами зведення називаються співвідношення, за допомогою яких значення тригонометричних функцій аргументів 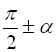, , ,  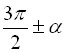виражаються через значення , , , .

Для полегшення запам’ятовування формул зведення можна користуватися такими правилами:

1) якщо у формулах містяться кути  і , то найменування функції не змінюється; якщо ж у формулах містяться кути  і , то найменування функції змінюється на подібне (синус – на косинус, тангенс – на котангенс і навпаки);

2) щоб визначити знак у правій частині формули («+» або « –»), досить, вважаючи кут  гострим, визначити знак виразу, який стоїть у лівій частині формули; при цьому перед функцією кута  ставлять такий знак, який має зведена функція кутів , , , .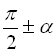

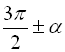Наприклад, ; .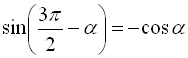

Приклад. Звести до тригонометричної функції гострого кута:

а) ; б) .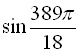

Розв’язання

Врахуємо, що період для  і  дорівнює  або .

а);

б)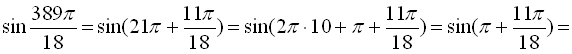 

.

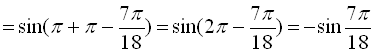Відповідь: а) ; б) .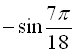

Графіки тригонометричних функцій

Синусоїда

Графіки функцій y = sin x та y = cos x розміщені в смузі, обмеженій прямими
y = -1   та   y = 1.

Тангенсоїда

Властивості тригонометричних функцій

Тригонометричні рівняння

Перегляньте відео про тригонометричні рівняння

Тригонометричні нерівності

Розв'яжіть нерівності і здайте мені на перевірку.